Mon site Jimdo
Un nombre parfait est un nombre égal à la somme de ses diviseurs propres.
Par exemple, 6 est parfait car ses diviseurs propres sont 1 ; 2 et 3.
Or 1 + 2 + 3 = 6.
On peut programmer la recherche de nombres parfaits.
Voici ce que cela peut donner avec Scratch (on peut surement optimiser...)
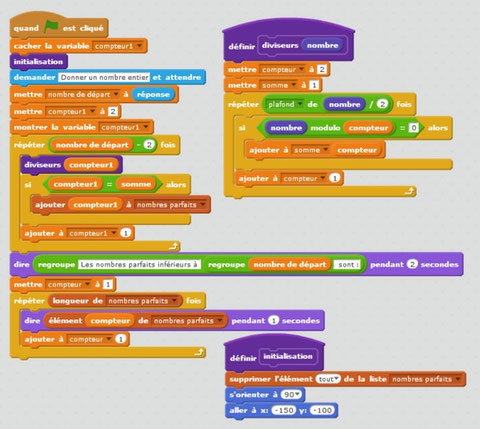
Il n'est pas inintéressant de programmer cela avec des élèves dès le collège.
Très vite cependant, les calculs sont longs et donc l'attente...
La programmation en Python est beaucoup plus simple, et les calculs plus rapides (même si pour le cas des nombres parfaits, on n'ira pas bien loin de toute façon !)
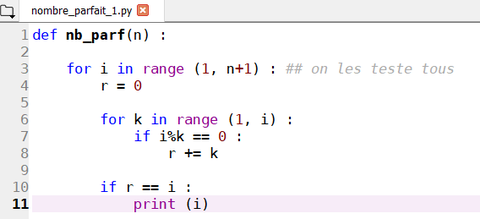
Une évolution possible est l'ajout d'une liste :
Écrire commentaire
El bhaitti (lundi, 22 juin 2020 03:51)
def par(n):
for i in range(1,n+1):
d=[]
for j in range(1,i):
if i%j==0:
d.append(j)
if sum(d)==i:
print(i)
print(par(1000))
HcPcEgmp (lundi, 29 novembre 2021 00:43)
20
HcPcEgmp (lundi, 29 novembre 2021 00:44)
20
HcPcEgmp (lundi, 29 novembre 2021 01:14)
20
HcPcEgmp (lundi, 29 novembre 2021 01:15)
20
HcPcEgmp (lundi, 29 novembre 2021 01:57)
20
HcPcEgmp (lundi, 29 novembre 2021 02:39)
20
HcPcEgmp (lundi, 29 novembre 2021 02:56)
20
thg (mercredi, 01 mars 2023 13:52)
hgxt
mox (mardi, 04 juillet 2023 20:57)
def par(n):
for i in range(1,n+1):
d=[]
for j in range(1,i):
if i%j==0:
d.append(j)
if sum(d)==i:
print(i)
print(par(1000000))
par (mardi, 04 juillet 2023 21:44)
print(par(1000000))
pHqghUme (dimanche, 29 septembre 2024 05:35)
20